01. たろちゃれ part 1(Taro さん)
2、3、4、5、6、7、8、9、10 で割った余りがすべて異なるような最小の自然数を求めなさい。
注:ちょうど割り切れるときの余りは 0 として考えてください。
〔解答・解説〕2~10 の最小公倍数は 2520 であるから、2519 以下の自然数について余りがすべて異なるものを考えれば十分である。
余りがすべて異なることに注意して樹形図を作ると、以下の 1)~3) の 3 通りが考えられる。
| 除数 | 2 | 4 | 6 | 8 | 10 | 3 | 5 | 7 | 9 | |
| 1) | 余り | 0 | 2 | 4 | 6 | 8 | 1 | 3 | 5 | 7 |
| 除数 | 2 | 4 | 6 | 8 | 10 | 3 | 5 | 9 | 7 | |
| 2) | 余り | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 | 0 |
| 3) | 余り | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 | 6 |
1) 2 を加えると 2~10 のすべてで割り切れるから、求める数は 2~10 の最小公倍数 2520 から 2 を引いた 2518 となる。
2) 1 を加えると除数 2、3、4、5、6、8、9、10 で割り切れるから、求める数は 2、3、4、5、6、8、9、10 の最小公倍数の 360 の倍数から 1 を引いたもの(359、719、1079、1439、1799、2159、2519)のうち、7 で割り切れる 1799 となる。
3) 1 を加えると 2~10 のすべてで割り切れるから、求める数は 2~10 の最小公倍数 2520 から 1 を引いた 2519 となる。
以上より、題意を満たす最小の自然数は 1799 である。
02. みんな解いてね !!(長野 美光 さん)
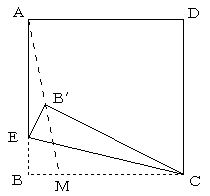
正方形 ABCD の辺 AB 上(両端は含まない)に点 E をとります。直線 CE で、この正方形を折り返すとき、点 B の移動先を点 B' とし、直線 AB' と辺 BC またはその延長線上との交点を M とします。
今、点 E を図の位置より少し上にとったとき、点 M が辺 BC の中点になりました。
このとき、三角形 AB'E の面積は、正方形 ABCD の面積の□倍になります。□に当てはまる数を既約分数(それ以上約分できない分数)で、答えてください。
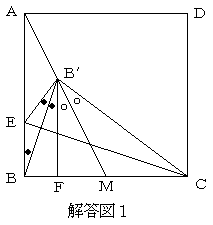
〔解答・解説〕解答図 1 のように、B' から辺 BC に下ろした垂線の足を F とし、B と B' を結ぶ。
EB=EB' と EB//B'F より、図の●で示した 3 つの角はいずれも等しい。
一方、B'F:FM=B'C:MC=2:1 より、B'F:B'C=FM:MC となり、角の二等分線の定理より、B'M は ∠FB'C の二等分線になる。
つまり、図の○で示した 2 つの角は等しい。
∠EB'C=90° であるから、∠BB'M=45° である。
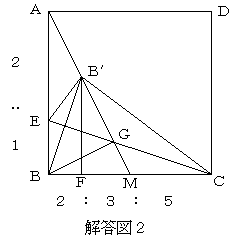
B'M と EC の交点を G とすると、折り返し図形の対称性から ∠B'BG=45° となり、BG は点 B から AM に下ろした垂線になる。
三角形 ABM、BGM、AGB は互いに相似で、AB:BM=BG:GM=AG:GB=2:1 より、MG:BG:AG=1:2:4
一方、BG=B'G なので、AM 上において、MG:GB':B'A=1:2:2
よって、BF:FM=AB':B'M=2:(2+1)=2:3
M は BC の中点なので、BF:FM:MC=2:3:5 となり、BF は BC の 1/5 倍の長さ…①
一方、FM は BF の 3/2 倍、B'F は FM の 2 倍なので、B'F は BF の 3/2×2=3 倍である。
三角形 BFB' と三角形 EBC は相似なので、EB:BC=BF:FB'=1:3
よって、AE:EB=2:1 となり、AE は AB の 2/3 倍の長さ…②
①、②より、三角形 AB'E は正方形 ABCD の 1/2×1/5×2/3=1/15 (倍) の面積となる。
03. 内接円-相似比と面積比-(川田 智之 さん)
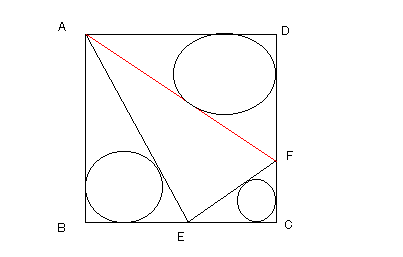
図のように、長方形 ABCD を AF に沿って折り返したところ、頂点 D は辺 BC 上の点 E に重なり、∠AEB=60° となりました。
図の中に 4 つの直角三角形ができますが、それぞれに内接する円のうち、最も大きな円と最も小さな円の面積比を答えてください。
〔解答・解説〕4 つの直角三角形は互いに相似で、直角以外の内角は 60° と 30° である。
DF=EF、EF:FC=2:1 より、DF:FC=EF:FC=2:1
また、AD=AE、AE:BE=2:1 より、AD:BE=2:1 であるから、E は BC の中点である。
したがって、4 つの直角三角形の面積は
(三角形 AFD)=(三角形 AEF)=(長方形 ABCD)×1/3
(三角形 AEB)=(長方形 ABCD)×1/4
(三角形 EFC)=(長方形 ABCD)×1/12
一般に、相似な三角形の相似比とその内接円の相似比は等しい。
よって、直角三角形の面積比とその内接円の面積比は一致する。
したがって、求める面積比は (最も大きな円):(最も小さな円)=(三角形 AFD):(三角形 EFC)=4:1 である。
04. カードゲーム(Y氏 さん)
1~8 の数字を、表と裏に異なる数字を書いてカードを 4 種類つくりました。4 種類のカードのそれぞれの面には違う数字が書かれ、重複する数字はないものとします。すなわち、4 種類のカードの両面、合計 8 面に 1~8 のすべての数字が使われていることになります。さらに、4 種類のカードに対してそれぞれ同じものを 4 枚ずつ作り、全部で 16 枚のカードを作りました。
この中からある 1 枚を取り除き、残りの 15 枚を表裏ランダムに並べました。(裏に書いている数字は解りません)その結果は
1、1、1、2、2、2、3、3、4、5、5、6、7、7、8
でした。さらにもう一度、ある 1 枚(1 回目に取り除いたカードとは限りません)を取り除き、残りの 15 枚を表裏ランダムに並べました。その結果は
1、2、2、3、3、4、4、4、5、5、5、6、6、7、8
でした。
これら 2 回の試行の結果から、何種類のカードの数字のペアが確定すると言えるでしょうか?カードの両面が確定するものの数字のペアを全て答えてください。
〔解答・解説〕同種類のカードは 4 枚しかないので、1 回目に注目すると、1 の裏は 4、6、8 のいずれかになる。同様にして、1 回目、2 回目の結果から、
- 1 の裏は 4、6、8 のいずれか…①
- 2 の裏は 4、6、8 のいずれか
- 4 の裏は 1、7、8 のいずれか
- 5 の裏は 1、7、8 のいずれか
となる。①において 2 回目に注目すると、1、8 の合計は 2 枚なので、この組合せは不可能。同様にして、
- 1 の裏は 4、6 のいずれか…②
- 2 の裏は 6、8 のいずれか…③
- 4 の裏は 1、7 のいずれか…④
- 5 の裏は 7、8 のいずれか…⑤
となる。さらに、②に注目し、1 の裏が 6 と仮定すると、③より 2 の裏は 8 となり、⑤より 5 の裏は 7 となる。ところが、この結果は ④に矛盾するので、1 の裏が 6 という仮定は誤り。したがって、1 の裏は 4 と決まる。その他のカードについては、(2-8,5-7,3-6)、(2-6,5-7,3-8)、(2-6,5-8,3-7) の 3 通りが考えられるが、両面が確定するカードはない。したがって、両面が確定するカードは 1-4 のみ。
05. こんなふうにしてみよう。(うっしー さん)
問 1:
ある 3 けたの整数があります。
この整数は 1 をたすと 2 で割り切れ、2 をたすと 3 で割り切れ、3 をたすと 4 で割り切れ、4 をたすと 5 で割り切れ、5 をたすと 6 で割り切れ、6 をたすと 7 で割り切れます。
この整数は何でしょう。
問 2:
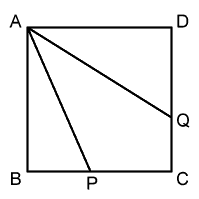
1 辺の長さがある長さの正方形 ABCD が図のようにあります。辺 BC 上に、線分 BP の長さが 5 cm となるように、点 P をとります。次に、点 A と点 P を直線で結びます。そして、角 DAP の二等分線と辺 DC との交点を Q とします。
このとき、線分 DQ の長さは 6 cm となりました。
では、線分 AP の長さは何 cm でしょう。
〔解答・解説〕
問 1:
1 を引くと 2~7 のすべてで割り切れるから、求める数は 2~7 の最小公倍数 420 の倍数に 1 を加えた数である。これを満たす 3 けたの整数は 421,841 である。
問 2:
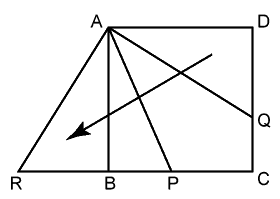
図のように、三角形 AQD を点 A を中心に時計回りに 90° 回転させ、点 Q が移った点を R とし、∠PAQ=□ とする。
このとき、∠QAD=□、∠AQD=90°-□、∠BAP=90°-□×2、∠RAB=□
よって、∠RAB+∠BAP=∠RAP=90°-□…①
また、∠ARB=∠AQD=90°-□…②
①、②より、三角形 PAR は PA=PR の二等辺三角形。
DQ=BR=6 cm、BP=5 cm より、AP=RP=RB+BP=11 (cm)
06. 天秤使いの妙技(キューダ さん)
重さが異なる 5 つの「重り」と「天秤」がありました。
A 君は、B 君に向かって
「君なら何回天秤を使って、重りを重い順に並べ替えられる?」
と聞きました。B 君は少し考え、
「うーん、…… 8 回かな」
と答えました。それに対し、A 君は
「7 回あれば、十分なんだよ」
とこたえ、重りを天秤に載せ始めました。
便宜上、重りには、A、B、C、D、E という名前を付けることにします。
最初の 3 回は、次のような操作をし、次のような結果を得ました。
1 回目:A と B を比べ A>B (A の方が B よりも重い) が判明
2 回目:C と D を比べ C>D が判明
3 回目:A と C を比べ A>C か判明
以下同様に、重りを 1 つずつ比較する操作を(確実に 7 回以内で終わるように)繰り返しましたが、なんと、6 回目の比較が終わった時、
「運が良かったこともあるけど、6 回で終わっちゃった。」
と言って、重い順番に並べ替えました。
さて、A 君が出した結論は、次の (1)~(15) のうちどれでしょうか?可能性があるものだけを全て挙げて下さい。
(1) ABCDE (2) ABCED (3) ABECD (4) ACBDE (5) ACBED
(6) ACDBE (7) ACDEB (8) ACEBD (9) ACEDB (10) AEBCD
(11) AECBD (12) AECDB (13) EABCD (14) EACBD (15) EACDB
〔解答・解説〕5 個のおもりの並び順は 5!=120 通り。また、27=128
よって、5!<27 が成り立つため、「うまく」天びんを使えば 7 回で可能となるのである。
しかし、120 と 128 はとても近い値であるため、「常に」無駄な比較を行わないことが要求される。その結果、比較する手順がかなり限定されることになる。
最初は 120 通りの可能性があり、これを 1 回目の比較で 60 通りに減らし、以下、30 通り、15 通りと減らしていく。ところが、4 回目に 15 通りが 9 通りか 6 通りに絞られるような比較を行ってしまうと、「確実に 7 回以内で終わる」という条件を満たせなくなるので失敗となる。なぜなら、もし 9 通りに絞られてしまうと、9>2³ なので、残り 3 回の比較では確定できなくなるからである。したがって、4 回目は 15 通りが 8 通り以内、すなわち、8 通りか 7 通りへ絞られるような比較を行わなければならない。そして、4 回目以降の比較による解の候補数の変移は、以下の 4 パターンが考えられる。
- 15 通り → 8 通り → 4 通り → 2 通り → 確定
- 15 通り → 7 通り → 4 通り → 2 通り → 確定
- 15 通り → 7 通り → 3 通り → 2 通り → 確定
- 15 通り → 7 通り → 3 通り → 確定
この問題では 6 回の比較で確定したということから、「15 通り → 7 通り → 3 通り → 確定」というパターンに限られる。
さて、最初の 3 回の比較の結果、可能性がある順番 (重い順) は以下の 15 通り:
ABCDE ABCED ABECD ACBDE ACBED ACDBE ACDEB ACEBD
ACEDB AEBCD AECBD AECDB EABCD EACBD EACDB
4 回目に比較する必要がある組合せは以下の 6 組:
(A,E)、(B,C)、(B,D)、(B,E)、(C,E)、(D,E)
(1 回目と 3 回目の結果から、A>D は明らか。)
この 6 組の比較のうち、上記 15 通りの場合を 8 通りまたは 7 通りに絞ることができるのは (C,E) の比較に限られ、7 通りになるのは E>C となる以下の場合である:
ABECD AEBCD AECBD AECDB EABCD EACBD EACDB
5 回目に比較する必要がある組合せは以下の 4 組:
(A,E)、(B,C)、(B,D)、(B,E)
(他の組合せの大小はすでに確定)
この 4 組の比較のうち、上記 7 通りの場合を 4 通りまたは 3 通りに絞ることができるのは (A,E) と (B,C) の比較で、3 通りになるのはそれぞれ E>A、B>C となる以下の場合である:
E>A のとき EABCD EACBD EACDB
B>C のとき ABECD AEBCD EABCD
よって、6 回目の比較で確定するのは
5 回目 E>A の場合:6 回目 B>C のとき EABCD、D>B のとき EACDB
5 回目 B>C の場合:6 回目 E>A のとき EABCD、B>E のとき ABECD
したがって、答えは ABECD,EABCD,EACDB の 3 通り。
08. 比と比との値(ヴェルデイ さん)
親子のカンガルーがいます。親カンガルーが 5 飛びする時間と、子カンガルーが 6 飛びする時間は同じです。親カンガルーが 3 飛びする長さと、子カンガルーが 4 飛びする長さは同じで、親カンガルーの 1 飛びする長さは 2 m です。
親子カンガルーが同じ場所にいるとき、次の問いに答えなさい。
先に飛び出した子カンガルーが 40 飛びした時、親カンガルーが出発しました。親カンガルーは、なんとびで飛び続ける子カンガルーに追いつきますか。
〔解答・解説〕子カンガルー 1 飛びの距離は 2×3÷4=1.5 (m) であるから、親カンガルーが飛び始めるとき、子カンガルーは 40×1.5=60 (m) 先に進んでいる。
また、親カンガルーは 1 とびあたり、2-1.5×6/5=0.2 (m) の差を縮める。
したがって、親カンガルーは 60÷0.2=300 (飛び) で子カンガルーに追いつく。
09. 国道沿いのラーメン屋(中村 明海 さん)
12 月 1 日、小樽市内の国道沿いにラーメン屋が 2 軒並んで開店しました。マサルさんが経営する M 店と、トモエさんが経営する T 店です。どちらも評判は上々で、ともに開店以来毎日客を増やし続けています。
では、集客を競い合うふたりの日記をごらん下さい。
トモエさんの日記より。
「今日 6 日、T 店には M 店より 100 人多くの客が来た。」
「今日 8 日の T 店の客の数は、M 店の 5 日~ 8 日の客の数の合計に等しい。」
マサルさんの日記です。2 日以降毎日同じことを書いています。
「昨日、M 店には、今日の両店の客の数の差の半分しか客が来なかったが、今日、M 店には、昨日の両店の客の数の和の半分も客が来た。」
さて、8 日に、T 店の客の数は M 店の何倍だったのでしょうか。もし割りきれない場合は、小数第 4 位以下を切り捨て小数第 3 位まで答えて下さい。
〔解答・解説〕両店とも客の数は増え続けた。もしある日、M 店の客の数より T 店の客の数が少ないと仮定すると、(マサルさんの日記の後半の記述から)翌日 M 店の客の数が減ることになってしまい、不都合である。したがって、マサルさんの日記における「両店の客の数の差」とは、T 店の客の数から M 店の客の数を引いたものとなる。
ある日の M 店の客の数を ○+○、T 店の客の数を △+△ とすると、(マサルさんの日記から)M 店の前日の客の数は △-○、翌日の客の数は △+○ となることが分かる。この 3 日間、M 店の客の数は △-○、○+○、△+○ と変化する。つまり、M 店の客の数には、「前日+当日=翌日」という関係があることが分かる。(このような関係を持つ数列をフィボナッチ数列という。)
6 日の客の数の差が 100 人だったので、その前日 5 日の M 店の客の数はその半分の 50 人である。そこで、最初の 5 日間の M 店の客の数の変化を考えてみる。
3 日の M 店の客の数を □ とし、「前日+当日=翌日」という関係から、M 店の客の数を次々にさかのぼって表してみる。
M 店の客の数:
- 5 日 50
- 4 日 50-□(5 日の 50 から 3 日の □ を引く)
- 3 日 □
- 2 日 50-□×2(4 日の 50-□ から 3 日の □ を引く)
- 1 日 □×3-50 (3 日の □ から 2 日の 50-□×2 を引く)
また、マサルさんの日記から、T 店の客の数は、翌日の M 店の客の数の 2 倍から、当日の M 店の客の数を引いたものになるので、次のようになる。
T 店の客の数:
- 4 日 50+□(50×2 から 50-□ を引く、以下同様)
- 3 日 100-□×3
- 2 日 □×4-50
- 1 日 150-□×7
さて、1 日から 2 日にかけて、両店とも客の数が増えたので、
M 店について、50-□×2>□×3-50 より、□<20
T 店について、□×4-50>150-□×7 より、□>200/11=18.1…
さらに、□ は整数であるから、□ は 19 と決まる。
このとき、両店の日々の客の数は
| 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | |
| M 店 | 7 | 12 | 19 | 31 | 50 | 81 | 131 | 212 |
| T 店 | 17 | 26 | 43 | 69 | 112 | 181 | 293 | 474 |
と定まり、題意を満たす。
したがって、8 日の両店の客の数の比は、474÷212=2.235…
(ちなみに、トモエさんの 8 日の日記は自明であり、参考にはならない。)
10. 仁義なき戦い(中学への算数にチャレンジ さん)
A、B、C の 3 人がジャンケンゲームをしました。勝負がつく(1 人だけが勝つ、2 人だけが勝つの 2 通りの場合があります)ときだけを考えて、あいこは考えないものとします。勝った回数がある決められた回数に達すると、その人はゲームから抜けて(2 人が同時に抜けてゲームが終わることもあります)、残った 2 人でどちらかが決められた回数だけ勝つまでゲームを続けます。
17 回目の勝負で A が勝って A が抜け、20 回目の勝負で B が勝って、ゲームは終わりました。
このとき、C が勝った回数は最も多い場合で何回ですか。
〔解答・解説〕3 人が勝った回数の合計で最も多いのは、最初から 17 回目までは 2 人が勝ち、18~20 回目は 1 人が勝つ場合であるから、2×17+3=37 回。
このとき、C が勝った回数が最も多くなるのは、A、B がそれぞれ 13 回、C が 11 回勝つ場合である。
この条件を満たす場合は存在する(下表が一例)ので、答えは 11 回。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| A | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | |||||||
| B | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | |||||||
| C | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
11. ゲームをしませんか?(ako さん)
A、B がゲームをくり返し行い優勝争いをしています。1 回のゲームで、A、B の勝つ確率はそれぞれ 1/3、2/3 です。
先に 3 勝した方が優勝するものとするとき、A が優勝する確率を求めて下さい。あいこは、無いことにします。
〔解答・解説〕A が優勝するのは以下の 3 通り。
1) A が 3 回目のゲームで優勝する場合:
A は最初の 3 回すべて勝てばよいから、1/3×1/3×1/3=1/27
2) A が 3 勝 1 敗で、4 回目のゲームで優勝する場合:
A は 3 回目まで 2 勝 1 敗で、4 回目に勝てばよいから、(1/3×1/3×2/3)×3×1/3=2/27
3) A が 3 勝 2 敗で、5 回目のゲームで優勝する場合:
A は 4 回目まで 2 勝 2 敗で、5 回目に勝てばよいから、(1/3×1/3×2/3×2/3)×6×1/3=8/81
したがって、A が優勝する確率は 1/27+2/27+8/81=17/81
12. 1 年間考えた割に簡単な問題(DrK さん)
3 cm 間隔で打ち付けられている 2 本の釘の一方に長さ 15 cm の糸を付け、その先に半径 3 cm の円盤を付けます。
糸を張った状態で、可能な限り円盤を回転させる時、
(1) 円盤が通って出来る領域の面積は何 cm² ですか?
(2) 円盤の中心の軌跡は何 cm ですか?
いずれも円周率は 3.14 とします。最終的な答えは小数第 3 位を四捨五入してください。尚、必要であれば、1 辺の長さが 2 cm の正三角形の高さ=1.732 cm、1 辺が 1 cm の直角二等辺三角形の斜辺の長さ=1.414 cm で計算してください。
注:円盤は釘に引っかかります。
〔解答・解説〕
(1) 釘の間隔と円板の半径が等しいことに注意すると、円板が通ることのできる部分には、1 辺の長さが 3 cm の正三角形のすき間が 2 つできる。
したがって、半径が 15+6=21 (cm) の円から、1 辺の長さが 3 cm の正三角形 2 つ分を取り除けばよいから、求める面積は 21×21×3.14-3×(1.732×3/2)÷2×2=1376.946 (cm²)
(2) 2 本の釘と円板の中心が一直線上にある状態から、糸を時計回りに釘にまきつけていくことにする。
はじめ、円板の中心は半径が 15+3=18 (cm) の円弧をえがく。半周したところで糸は釘に引っかかり、半径が 18-3=15 (cm) の円をえがき始める。同様に、半周えがくたびに 3 cm ずつ円の半径は小さくなっていき、ついには、糸が完全に釘にまきつくことになる。そして、円板がもう一方の釘に引っかかるまで、円板を釘の周りに回転させるとき、円板の中心は半径 3 cm、中心角 120° の円弧をえがく。
同様にして、はじめの状態から反時計回りに糸をまきつけていくことができる。
したがって、求める長さは (18+15+12+9+6)×2×3.14+3×2×3.14×2/3=124×3.14=389.36 (cm)
13. たぶん一番簡単な問題(清川 育男 さん)
5、5、24、24 を 1 回ずつ使い、四則演算によって 120 を作ってください。四則演算とは、+、-、×、÷ を使った計算のことです。( ) は使ってもよいが無駄な使用は不可。例えば (24+5)+(5+24) は、24+5+5+24 としてください。
注:小学校で習う範囲の知識だけで解いてください。
〔解答〕24÷(5-24÷5)
14. タイル張り職人の銀次郎くん (\^o^)(萬田銀次郎(ミナミの鬼) さん)

銀次郎くんは全く同じ大きさの正方形の赤いタイルと青いタイルをたくさん持っています。これらのタイルを 9 枚用いて右の図のようなたて、よこともに 3 枚ずつの正方形の模様を作ろうと思います。また模様は自由に回転させることはできますが、裏返すことはできません。
使わない色のタイルがあっても構わないとき、銀次郎くんは何通りの模様を作ることができますか。
〔解答・解説〕
- 赤 0 枚、青 9 枚の場合、1 通り。
- 赤 1 枚、青 8 枚の場合、3 通り。
- 赤 2 枚、青 7 枚の場合、10 通り。
- 赤 3 枚、青 6 枚の場合、22 通り。
- 赤 4 枚、青 5 枚の場合、34 通り。
- 赤 5 枚、青 4 枚の場合、34 通り。
- 赤 6 枚、青 3 枚の場合、22 通り。
- 赤 7 枚、青 2 枚の場合、10 通り。
- 赤 8 枚、青 1 枚の場合、3 通り。
- 赤 9 枚、青 0 枚の場合、1 通り。
以上を合わせて、(1+3+10+22+34)×2=140 (通り)
15. Yamanote LOOP(Nagahiro、Y. さん)
山手線は全部で 29 駅あり総延長は 35 km です。それを平均時速 32 km で電車が回る環状線です。(約 1 時間で一周するわけですね)
200X 年 4 月、山手線に快速電車を走らせることになりました。停車させる駅は 4 駅に決まりました。また快速停車駅間には少なくともひとつの通過駅があるようにします。
(1) 東京駅が快速電車の停車駅として確定した場合、残りの 3 駅の決め方は何通りありますか。
(2) 確定している停車駅がない場合、4 つの停車駅の決め方は何通りありますか。
〔解答・解説〕
(1) 29 の駅に次のように番号をふる。東京駅を 1 として、時計回りに 2、3、…、29 とする(有楽町は 2、秋葉原は 28 となる)。
残り 3 つの停車駅の番号を x、y、z (x<y<z) とすると、3≦x<y-1<z-2≦26 である。
これを満たす x、y、z の組の個数は、3、4、5、…、26 の 24 個から 3 つを選んで作られる組合せの個数であるから、24×23×22÷6=2024 (通り)
(2) 第一の停車駅を決めてから残りの 3 つの停車駅を決めると考えると、(1) の結果から、2024×29÷4=14674 (通り)
(4 で割るのは、第一の駅を決めるときに重複して 4 回数えられることを除外するため。)
16. マージャンパイ(杉本 未来 さん)
下の 28 マスのうち、同じ 4 種類の画像が入っているマスは 1 組しかありません。
その組み合わせを探してください。ただし、4 種類の置き場所は関係ないものとします。
| 1 | 2 | 3 | 4 | |
| A | ||||
| B | ||||
| C | ||||
| D | ||||
| E | ||||
| F | ||||
| G |
〔解答・解説〕1) 東も南もふくむ場合:
| 1 | 2 | 3 | 4 | |
| A | 東南西北 | 南北白東 | ||
| B | 南西東中 | |||
| C | 東南白発 | |||
| E | 南西発東 | |||
| F | 発中東南 | |||
| G | 南北中東 | 中東南白 |
東、南以外の組合せは
A1 西北 A4 北白 B4 西中 C1 白発
E2 西発 F2 発中 G3 北中 G4 中白
であるが、この中に同じ組合せはない。
2) 東をふくみ、南をふくまない場合:
| 1 | 2 | 3 | 4 | |
| A | 北中東西 | |||
| B | 北東白中 | |||
| C | 東西北発 | |||
| D | 白発中東 | 中東西発 | 発東西白 | |
| F | 発東北白 |
東以外の組合せは
A3 北中西 B1 北白中 C4 西北発 D1 白発中
D2 中西発 D3 発西白 F4 発北白
であこのうち、西をふくむものは
A3 北中西 C4 西北発 D2 中西発 D3 発西白
また、西をふくまないものは
B1 北白中 D1 白発中 F4 発北白
いずれの場合も同じ組合せはない。
3) 東をふくまず、南をふくむ場合:
| 1 | 2 | 3 | 4 | |
| B | 中南北白 | 発中南白 | ||
| C | 南北中発 | |||
| D | 北中南西 | |||
| E | 西発中南 | |||
| F | 南西北白 | 発南西北 | ||
| G | 南西白発 |
南以外の組合せは
B2 中北白 B3 発中白 C2 北中発 D4 北中西
E3 西発中 F1 西北白 F3 発西北 G2 西白発
であり、このうち、西をふくむものは
D4 北中西 E3 西発中 F1 西北白 F3 発西北 G2 西白発
また、西をふくまないものは
B2 中北白 B3 発中白 C2 北中発
いずれの場合も同じ組合せはない。
4) 東も南もふくまない場合:
| 1 | 2 | 3 | 4 | |
| A | 中北白発 | |||
| C | 白発西北 | |||
| E | 西白発中 | 白中西北 | ||
| G | 中北西白 |
まず、西をふくまない A2 がはずれる。残りの 4 つのうち、北をふくまない E1 もはずれる。さらに、残りの 3 つを調べれば、同じ 4 種類の画像が入っているマスは E4,G1 であることが分かる。
17. 立体図形 ?!(CRYING DOLPHIN さん)
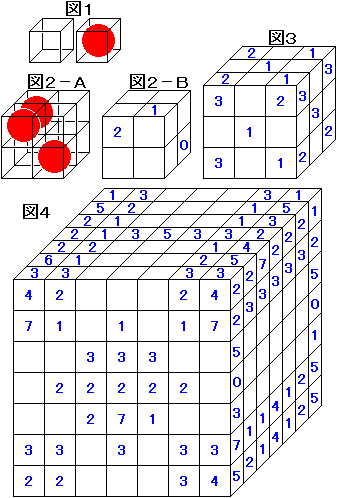
図 1 のような、透明な同じ大きさの立方体の小箱がたくさんあり、小箱の各面の中心には小さな穴があいています。また、いくつかの小箱には、各面に内接する粘土製の赤玉が入っています。これから、小箱をすき間なく積み重ねて立方体を作ります。そして、次のような操作を考えます。
まず、長くてまっすぐで細い針金を一本用意します。小箱を積み重ねて作った立方体の表面に出ている小箱の面をひとつ選び、その面にあいている穴に針金を通し、立方体の反対側まで通します。そして、針金を最初に通した面に、"針金が貫通した赤玉の数" を記入します。例えば、図 2-A のように小箱 8 個で立方体を作ったとき、図 2-B は小箱の面のいくつかに数字を記入したものです。もちろん、針金は折り曲げることはできないものとして、次の問いに答えなさい。なお、「解なし」が正解のものはありません。
(1) 27 個の小箱をすき間なく積み重ねて立方体を作りました。図 3 は、表面に出ている小箱の面に数字をいくつか記入したものです。このとき、赤玉の入った小箱は何個あると考えられますか。
(2) 343 個の小箱をすき間なく積み重ねて立方体を作りました。図 4 は、表面に出ている小箱の面に数字をいくつか記入したものです。このとき、赤玉の入った小箱は何個あると考えられますか。
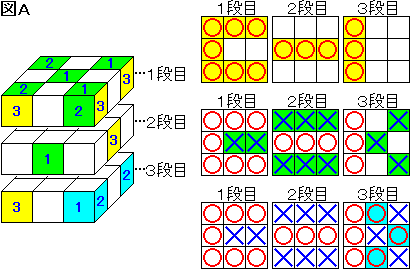
〔解答・解説〕
(1) これは地道に調べていくことにする。
"3" と書いてある方向の小箱には、すべて赤玉が入っている。
図 A で 黄→緑→水色 の順に調べていくことにより、赤玉の入った小箱の位置がすべて特定されるので、赤玉の入った小箱は 16 個と分かる。
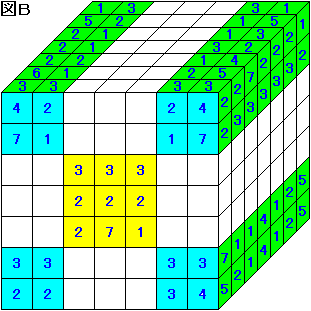
(2) (1) は小箱の数が少なかったので、地道に調べてできたが、今度は普通に調べていくと大変なことになりそうである。
そこで、問われているのは「赤玉の入った小箱の数」であって、赤玉の入った小箱の具体的な置き方ではないことに注目する。
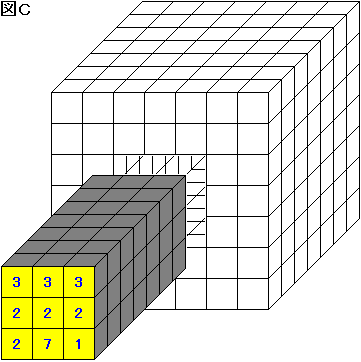
図 C において、灰色の 63 個の小箱のうち、赤玉の入った小箱の数は 1+3×3+2×4+7=25
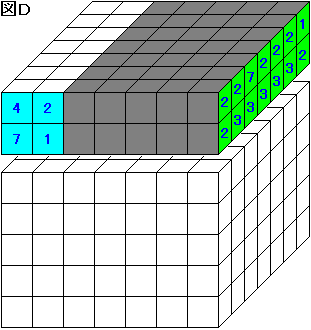
次に、図 D で灰色の 70 個の小箱について考える。
緑部分の数字の和 1+2×7+3×5+7=37 から、水色部分の数字の和 1+2+4+7=14 を引けばよい。
よって、赤玉の入った小箱の数は 37-14=23
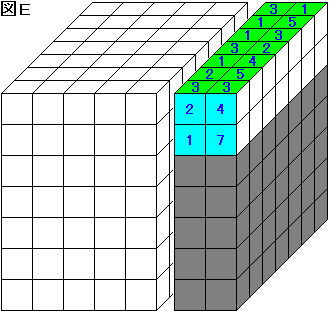
同様に、図 E の灰色の部分では、(1×4+2×2+3×5+4+5×2)-(1+2+4+7)
=23 が赤玉の入った小箱の数である。
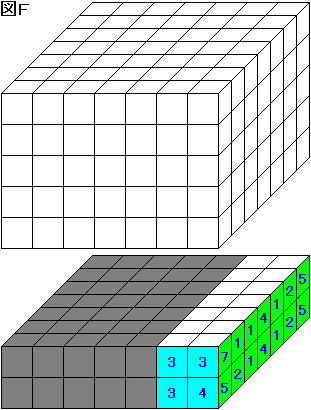
図 F の灰色の部分では、(1×5+2×3+4×2+5×3+7)-(3×3+4)=28 が赤玉の入った小箱の数である。
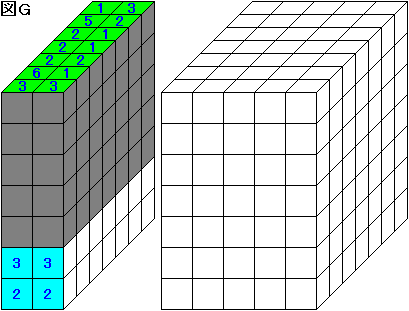
図 G の灰色の部分では、(1×4+2×5+3×3+5+6)
-(2×2+3×2)=24 が赤玉の入った小箱の数である。
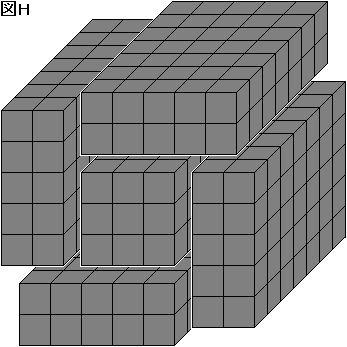
以上で、すべての小箱について調べたことになる。
したがって、答えは 25+23+23+28+24=123 (個)
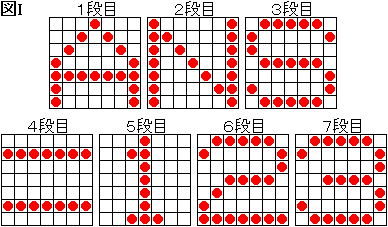
〔参考〕赤玉の入った小箱の配置例は図 I のようなものがあります。
具体的配置の一意性は確認していません。
18. 6 人の偶然 !?(たこやき大学 さん)
ある円形の池の円周上のコースを A~F の 6 人がまわります。6 人は同じ地点から同時に出発し、A~C は左回りに D~F は右回りにまわります。またそれぞれの速さは、左回りでは C が一番速く次に B、A の順になっています。右回りでは F が一番速く次に E、D の順になっています。さらに B は A と C の平均の速さで、C と E は同じ速さです。
さて、出発してから誰も 1 周しないうちに 6 人の位置関係が見事な正六角形になりました。
このとき、6 人の速さの比 A:B:C:D:E:F を最も簡単な整数の比で求めなさい。ただし 6 人は一定の速さでまわるものとします。
〔解答・解説〕B は A と C の中間に位置し、C と E はスタート地点から等距離にある。
また、A~C、D~F の速さの関係に注意し、だれも 1 周していないことから、正六角形はスタート地点から左回りに FEABCD と一意に定まり、スタート地点は弧 DF の中点となる。
したがって、速さの比は A:B:C:D:E:F=5:7:9:1:9:11
19. がんばれ F 君(BossF さん)
F 君は塾が遠いので、お母さんに車で送り迎えしてもらってます。行きはいいのですが、帰りは残されることが多いので、本当は 7 時に終わるのですが、余裕を見た待ち合わせ時刻を決めています。
さてある日、珍しく時間通りに終わった F 君は
「一本道だから、歩いて帰っても、お母さんに会えるや」
とおもって、とことこと歩いて帰りました。そして無事お母さんに出会い、早く終わったことを誉められるかと思ったら
「あんた、ほんとにばかね~。ここから車に乗っても、塾で待ってたのと家に着く時間は 6 分しか違わないじゃない」
といわれて、シュンとなってしまいました。
では、いつも二人が、待ち合わせている時刻は?ただし、F 君の歩く速さは毎時 4 km、お母さんの車の速さは毎時 60 km とします。
〔解答・解説〕家に着く時刻は、二人が出会った地点 P と塾の間を車で往復する時間だけ早くなるから、地点 P と塾の距離は 60×6/60÷2=3 (km)
よって、F 君が歩いた時間は 3÷4×60=45 (分) であり、待ち合わせの時刻は F 君が出発してから 45+3=48 (分後) となる。
したがって、答えは 7 時 48 分。
20. 4 個のエジプト分数の和の最大値(ノースダウン さん)
1 より大きく、相異なる 5 個の正整数 a、b、c、d、e が次の関係を満たすとき、e がとり得る最大の値を求めよ。
1/a+1/b+1/c+1/d=e/999999
注:右辺の条件は、e が 1 より大きい正整数であることのみであり、既約分数であることといった条件はありません。
〔解答・解説〕簡単のため、f=1/a+1/b+1/c+1/d とおく。
また、a<b<c<d として十分である(一般性を失わない)。
(a,b,c,d)=(2,3,6,7) 以外の組合せのとき、f が 8/7(=1.1428…) より小さいか、f×999999(=e) が整数にならないことを示す。
1) a>2 の場合:
(a,b,c,d)=(3,4,5,6) のとき、f は最大値 0.95 をとるが、これは 8/7 より小さい。
2) a=2、b>3 の場合:
(a,b,c,d)=(2,4,5,6) のとき、f は最大値 1.11… をとるが、これは 8/7 より小さい。
3) a=2、b=3 で、かつ
3-a) c=4 の場合:
5≦d≦16 のとき、f>8/7 となるが、f×999999 は整数にならない。
3-b) c=5 の場合:
6≦d≦9 のとき、f>8/7 となるが、f×999999 は整数にならない。
3-c) c>5 の場合:
c=6、d=7 のとき、f は最大値 8/7 をとり、f×999999=8/7×999999=1142856
以上より、(a,b,c,d)=(2,3,6,7) のとき、e は最大値 1142856 をとる。
21. 解けない人は正確に作図してね(ぶぶおパパ さん)
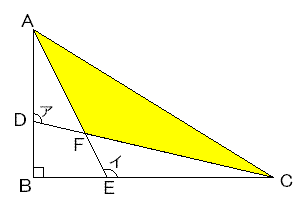
図のように、直角三角形 ABC の辺 AB 上に点 D、辺 BC 上に点 E をとり、2 直線 AE、CD の交点を F とします。
AD=5 cm、DB=3 cm、BE=4 cm、角ア+角イ=225 度のとき、三角形 AFC の面積は何 cm² でしょうか?
注:図はやや不正確です。
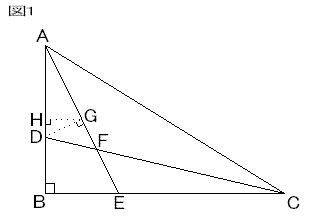
〔解答・解説〕図 1 のように、D から AE に垂線を引き、AE との交点を G とする。さらに、G から AB に垂線を引き、AB との交点を H とする。
3 つの三角形 ABE、GHD、AHG は相似で、AB:BE=8:4=2:1 より、GH:HD=AH:HG=2:1
よって、AH:HD=4:1
AD=5 cm であるから、AH=4 cm、HD=1 cm となり、HG=2 cm であることが分かる。
次に、∠ア+∠イ=225° に注目する。
四角形 DBEF の内角のうち、∠B=90°
また、∠D+∠E=180×2-225=135°
よって、∠F=360-90-135=135°
したがって、∠DFG=180-135=45° となり、∠GDF=45°
以上により、三角形 GDF は GD=GF の直角二等辺三角形である。
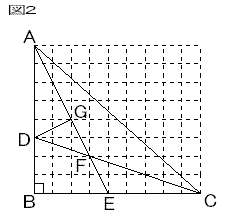
そこで、図 2 のように、1 cm 間隔の方眼上にこの図をえがいてみる (ここから図が正確になります)。
三角形 ABC の面積は 9×8÷2=36 (cm²)
三角形 ABE の面積は 4×8÷2=16 (cm²)
三角形 FEC の面積は 5×2÷2=5 (cm²)
したがって、三角形 AFC の面積は 36-16-5=15 (cm²)
22. あやのときめきメモリアル問題♪(あやのりん さん)
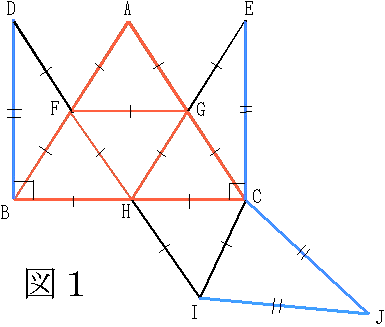
(1) 図 1 のような展開図を組み立てた立体 (ア) を考えます。この立体の体積は、図 1 の中の赤い部分(正三角形 ABC)を組み立てた正四面体 (イ) の体積の何倍になるでしょう?なお、青色の辺 DB、EC、CJ、IJ の長さは等しく、その他の辺の長さは全て等しくなっています。また、∠DBC=∠ECB=90 度で、DI、HE は一直線です。
(2) さて、ここであやのりんは、立体 (ア) に日本酒が入っていることを発見しました。今、立体 (ア) は三角形 HIC が底面となっており、日本酒は丁度半分の高さまであったそうです。そこで、あやのりんはその日本酒が飲みたくて、どうやってばれないようにこっそり飲もうか考えました。まず、それをメスシリンダーで正確に量ったところ 59.8 ml あったそうです。そして、今度は三角形 DBF を底面として立体 (ア) の丁度半分の高さになるようにちょびっと飲んだそうです。さて、あやのりんは日本酒を何 ml 飲むことが出来たでしょう?
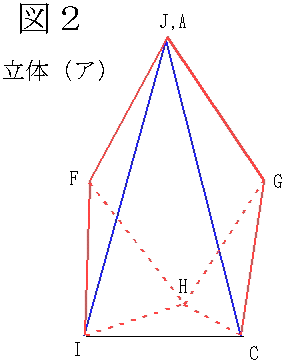
〔解答・解説〕
(1) 図 1 の展開図を組み立てると、図 2 のような立体 (ア) が完成する(A、F、H、G は同一平面上にある)。
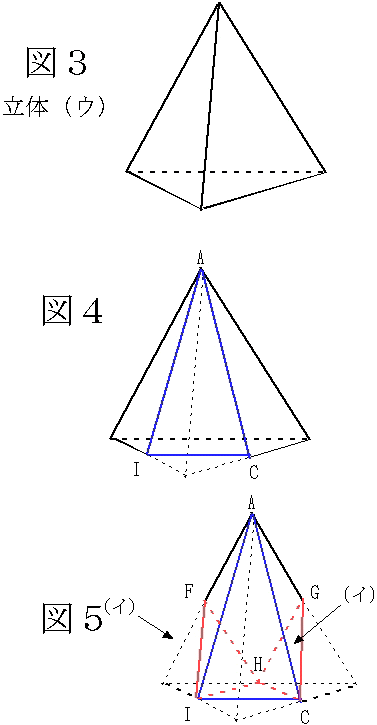
これは、図 3 のように正三角形 ABC を一つの面としてできる正四面体 (ウ) から、図 4 → 図 5 のように取り除いたものとなる。F、I、C、G はぞれぞれ各辺の中点である。
したがって、図 3 の正四面体 (ウ) は正三角形 ABC を組み立ててできる正四面体 (イ) の 2×2×2=8 (倍) であり、図 4 において底面積が 3/4 倍となり、図 5 において小さい正四面体 (イ) が 2 つ取り除かれるので、8×3/4-2=4 (倍) である。
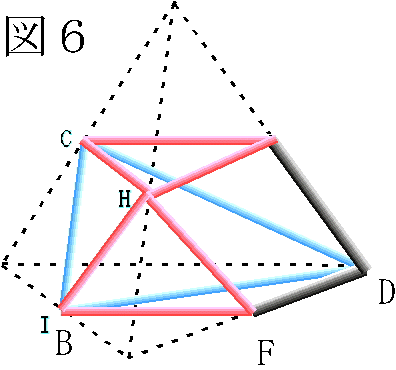
(2) 小さい正四面体 (イ) の体積を 1 とすると、立体 (ア) の体積は 4、大きい正四面体 (ウ) の体積は 8 となる。
立体 (ア) は三角形 HIC を底面におくと図 5 のようになり、高さがちょうど半分である日本酒の水面は F、G の位置にある。よって、はじめに入っていた日本酒の量は 8×7/8-1-1-2×7/8=13/4 であり、これが 59.8 ml に相当する。
次に、三角形 DBF を底面におくと図 6 のようになり、その高さは正四面体 (ウ) の 1/2 になるため、飲み終わったあとの高さは (ウ) の 1/4 となる。
よって、飲んだ後の体積は
8-8×(3×3×3)/(4×4×4)-(1+2)×7/8=2
したがって、あやのりんがこっそり飲んだ日本酒の量は 13/4-2=5/4
すなわち、59.8×5/13=23 (ml)
ほんとにちょびっとですね。。。(^^ゞ
23. イー・リャン・サン・スー……(POI さん)
長方形(正方形を含む)状にならべた○のなかに 1 から順に数を書き入れていきます。1 は必ず左上の○に書き、また、1 のとなりには 2 を、2 のとなりには 3 を、…… と連続する数は必ずとなりあうようにします。(となりあうとは、上下または左右にならんでいる○のことを指します。)たとえば、![]() のようにならべたときは、
のようにならべたときは、![]() と
と ![]() の 2 通りの書き入れ方があります。
の 2 通りの書き入れ方があります。
このとき、![]() のようにならべたときは ( ア ) 通りの書き入れ方があり、
のようにならべたときは ( ア ) 通りの書き入れ方があり、 のようにならべたときは ( イ ) 通りの書き入れ方があります。
のようにならべたときは ( イ ) 通りの書き入れ方があります。
〔解答・解説〕
(ア)
|
|
|
の 3 通り。
(イ) すべての場合を調べ上げる。1 から整数を書き入れていき、その後の書き入れ方がただ一通りに定まる場合は x で表すことにする。
| 1 | 2 | 3 | x |
| x | x | 4 | x |
| x | x | x | x |
の 1 通り。
| 1 | 2 | 3 | 4 |
| x | x | 6 | 5 |
| x | x | x | x |
の 1 通り。
| 1 | 2 | 3 | 4 |
| o | o | o | 5 |
| o | o | o | 6 |
において、o の部分は (ア) の書き入れ方にならって、3 通り。
| 1 | 2 | o | o |
| 4 | 3 | o | o |
| x | x | o | o |
において、o の部分は (ア) の書き入れ方にならって、3 通り。
| 1 | 2 | x | x |
| x | 3 | 4 | x |
| x | x | x | x |
の 1 通り。
| 1 | x | x | x |
| 2 | x | 6 | x |
| 3 | 4 | 5 | x |
の 1 通り。
| 1 | o | o | o |
| 2 | o | o | o |
| 3 | 4 | 5 | 6 |
において、o の部分は (ア) の書き入れ方にならって、3 通り。
| 1 | x | x | x |
| 2 | 5 | 6 | x |
| 3 | 4 | x | x |
の 1 通り。
| 1 | 6 | o | o |
| 2 | 5 | o | o |
| 3 | 4 | o | o |
において、o の部分は (ア) の書き入れ方にならって、3 通り。
以上を合わせて、1+1+3+3+1+1+3+1+3=17 (通り)
24. ははは(fumio さん)
ひとつのさいころをふって奇数の目が出たら続けてふり、偶数の目が出たら終わり、出た目の数の合計を得点とするゲームがあります。
このゲームをすると 1 の目が 1 回も出なくて得点が 30 点になりました。
このとき 3 の目が出た回数の最大と最小、5 の目が出た回数の最大と最小をそれぞれ求めなさい。
〔解答・解説〕最後に出る目は必ず偶数であることに注意して場合分けをする。
1) 最後に出る目が 2 の場合:
3 の目が 1 回と 5 の目が 5 回 または 3 の目が 6 回と 5 の目が 2 回
2) 最後に出る目が 4 の場合:
3 の目が 2 回と 5 の目が 4 回 または 3 の目が 7 回と 5 の目が 1 回
3) 最後に出る目が 6 の場合:
3 の目が 3 回と 5 の目が 3 回 または 3 の目が 8 回と 5 の目が 0 回
以上より、3 の目が出た回数の最大は 8、最小は 1 で、5 の目が出た回数の最大は 5、最小は 0 である。
25. 紙を切る(ヒデー王子 さん)
たて 1392 cm、よこ 2352 cm の長方形の紙 A から一辺の長さが 1 cm より長い正方形の紙を、次の 2 通りの方法で切り取っていくとき、各問いに答えよ。
(1) 長方形の紙 A から出来るだけ大きい正方形を切り取り、残った部分からも出来るだけ大きい正方形を切り取る。これを繰り返すと、最後に正方形を切り尽くして、長方形は全ていろいろな大きさのいくつかの正方形に切り分けられる。このとき合計何個の正方形が出来るか。例えば、たて 4 cm、よこ 6 cm の長方形からは、一辺 4 cm の正方形が 1 個、一辺 2 cm の正方形が 2 個、合計 3 個の正方形が出来ると考えられる。
(2) 長方形の紙 A から同じ大きさの正方形を、紙にあまりのないように切り取り尽くすとき、全部で何通りの切り取り方があるか。例えば、たて 4 cm、よこ 6 cm の長方形からは、一辺 2 cm の正方形を切り取る方法しかあり得ず 1 通りとなる。
〔解答・解説〕
(1) いわゆる「ユークリッドの互除法」による。
- 2352÷1392=1 あまり 960
- 1392÷960=1 あまり 432
- 960÷432=2 あまり 96
- 432÷96=4 あまり 48
- 96÷48=2
したがって、1+1+2+4+2=10 (個)
(2) (1) より、1392 と 2352 の最大公約数は 48 である。
正方形の 1 辺の長さは 1 cm より長いから、48、48/2、48/3、48/4、…、48/47 cm の 47 通り
26. 虎にお茶をかけるとどうなるでしょう?(かぶとっ さん)

答えはウサギになります。
A、B、E、G、I、R、T を求めて下さい。ただし A、B、E、G、I、R、T には異なる 1 桁の整数が入ります。答えが複数ある時はコンマ (,) で区切って書いてください。
| T | I | G | E | R | |
| x | T | ||||
| a | b | ||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| i | j | ||||
| R | A | B | B | I | T |
〔解答・解説〕T と R に注目して、T に入りうる数字を考える。
そのそれぞれの T に対して場合分けをする。
R を決定し、次は I に注目してすべての条件をみたす組合せを見つける。
| 5 | I | G | E | R | |
| x | 5 | ||||
| a | b | ||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| 2 | 5 | ||||
| R | A | B | B | I | 5 |
| 2 | I | G | E | R | |
| x | 2 | ||||
| a | b | ||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| 4 | |||||
| R | A | B | B | I | 2 |
まず、T について考える。
1) T=2 の場合:
I にどんな数字を入れても R=0 となるので、T≠2
同様の理由で、T≠1
次に、一の位に注目すると、R×T=T である。
2) T=5 の場合:
R は奇数となるが、I にどんな数字を入れても、R=2 となるので、T≠5
| 6 | I | G | E | 1 | |
| x | 6 | ||||
| 6 | |||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| 3 | 6 | ||||
| R | A | B | B | I | 6 |
| T | I | G | E | 1 | |
| x | T | ||||
| a | b | ||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| i | j | ||||
| R | A | B | B | I | T |
3) T=7、9 の場合:
R=1 となるが、i j=49、81 となり、いずれの場合も R≠1 であるから、T≠7、9
4) T=6 の場合:
R=1 となるが、I にどんな数字を入れても、R=3 または 4 となるので、T≠6
| 8 | I | G | E | 6 | |
| x | 8 | ||||
| 4 | 8 | ||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| 6 | 4 | ||||
| 6 | A | B | B | I | 8 |
5) T=8 の場合:
R=6 となる。
答えの十万の位が 6 であるから、g≦5
よって、I≦7
また、十の位に注目すると、d は偶数となるので、I も偶数である。
よって、I=0、2、4
| 8 | 0 | G | 7 | 6 | |
| x | 8 | ||||
| 4 | 8 | ||||
| 5 | 6 | ||||
| e | f | ||||
| 0 | |||||
| 6 | 4 | ||||
| 6 | 4 | B | B | 0 | 8 |
| 8 | 0 | G | 2 | 6 | |
| x | 8 | ||||
| 4 | 8 | ||||
| 1 | 6 | ||||
| e | f | ||||
| 0 | |||||
| 6 | 4 | ||||
| 6 | 4 | B | B | 0 | 8 |
5-1) I=0 の場合:
E=2 または 7 となる。
5-1-1) E=2 の場合:
百、千の位に注目すると、G×8+6=BB
これを満たす G は 8 であるが、B=R=6 となるので、E≠2
5-1-2) E=7 の場合:
百、千の位に注目すると、G×8+6=BB
これを満たす G は 2 であるが、B=G=2 となるので、E≠7
5-1-1)、5-1-2) より、I≠0
| 8 | 2 | G | 1 | 6 | |
| x | 8 | ||||
| 4 | 8 | ||||
| 8 | |||||
| e | f | ||||
| 1 | 6 | ||||
| 6 | 4 | ||||
| 6 | A | B | B | 2 | 8 |
5-2) I=2 の場合:
E=1 となる。
百、千の位に注目すると、G×8+61=BB または 100+BB
これを満たす G は 9 であるが、A=R=6 となるので、I≠2
(G=2 も満たすが、I=2 であるから不適)
| 8 | 4 | G | 5 | 6 | |
| x | 8 | ||||
| 4 | 8 | ||||
| 4 | 0 | ||||
| e | f | ||||
| 3 | 2 | ||||
| 6 | 4 | ||||
| 6 | A | B | B | 4 | 8 |
| 8 | 4 | G | 0 | 6 | |
| x | 8 | ||||
| 4 | 8 | ||||
| 0 | |||||
| e | f | ||||
| 3 | 2 | ||||
| 6 | 4 | ||||
| 6 | A | B | B | 4 | 8 |
5-3) I=4 の場合:
E=0 または 5 となる。
5-3-1) E=0 の場合:
百、千の位に注目すると、G×8+20=BB
これを満たす G は 3 であるが、B=I=4 となるので、E≠0
5-3-2) E=5 の場合:
百、千の位に注目すると、G×8+24=BB
これを満たす G は 8 であるが、B=G=8 となるので、E≠5
5-3-1)、5-3-2) より、I≠4
したがって、5-1)~5-3) より、T≠8
| 3 | I | G | E | 1 | |
| x | 3 | ||||
| 3 | |||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| 9 | |||||
| 1 | A | B | B | I | 3 |
6) T=3 の場合:
R=1 となる。
答えの十万の位が 1 であるから、g≧1
よって、I≧4
I=5 の場合、十の位の計算により E=5 となるから不適。
また、I≧7 の場合 A=T=1 となるから不適。
よって、I=4、6
| 3 | 6 | G | 2 | 1 | |
| x | 3 | ||||
| 3 | |||||
| 6 | |||||
| e | f | ||||
| 1 | 8 | ||||
| 9 | |||||
| 1 | A | B | B | 5 | 3 |
| 3 | 4 | G | 8 | 1 | |
| x | 3 | ||||
| 3 | |||||
| 2 | 4 | ||||
| e | f | ||||
| 1 | 2 | ||||
| 9 | |||||
| 1 | A | B | B | 4 | 3 |
6-1) I=4 の場合:
E=8 となる。
百、千の位に注目すると、G×3+22=BB
これを満たす G は 0 であるが、A=G=0 となるので、I≠4
6-2) I=6 の場合:
E=2 となる。
百、千の位に注目すると、G×3+8=BB
これを満たす G は 1 であるが、T=1 であるから I≠6
したがって、6-1)、6-2) より、T≠3
| 4 | I | G | E | 1 | |
| x | 4 | ||||
| 4 | |||||
| c | d | ||||
| e | f | ||||
| g | h | ||||
| 1 | 6 | ||||
| 1 | A | B | B | I | 4 |
7) T=4 の場合:
R=1 となる。
十の位に注目すると、d は偶数となるので、I も偶数である。
よって、I=0、2、6、8
| 4 | 0 | G | 5 | 1 | |
| x | 4 | ||||
| 4 | |||||
| 2 | 0 | ||||
| e | f | ||||
| 0 | |||||
| 1 | 6 | ||||
| 1 | 6 | B | B | 0 | 4 |
7-1) I=0 の場合:
E=5 となる。
百、千の位に注目すると、G×4+2=BB
これを満たす G は 5 であるが、E=5 であるから I≠0
| 4 | 2 | G | 8 | 1 | |
| x | 4 | ||||
| 4 | |||||
| 3 | 2 | ||||
| e | f | ||||
| 8 | |||||
| 1 | 6 | ||||
| 1 | A | B | B | 2 | 4 |
| 4 | 2 | G | 3 | 1 | |
| x | 4 | ||||
| 4 | |||||
| 1 | 2 | ||||
| e | f | ||||
| 8 | |||||
| 1 | 6 | ||||
| 1 | A | B | B | 2 | 4 |
7-2) I=2 の場合:
E=3 または 8 となる。
7-2-1) E=3 の場合:
百、千の位に注目すると、G×4+81=BB または 100+BB
これを満たす G は存在しないので、E≠3
7-2-2) E=8 の場合:
百、千の位に注目すると、G×4+83=BB または 100+BB
これを満たす G は 7 であるが、B=R=1 となるので E≠8
(G=4 も満たすが、T=4 であるから不適)
7-2-1)、7-2-2) より、I≠2
| 4 | 6 | G | 9 | 1 | |
| x | 4 | ||||
| 4 | |||||
| 3 | 6 | ||||
| e | f | ||||
| 2 | 4 | ||||
| 1 | 6 | ||||
| 1 | 8 | B | B | 6 | 4 |
7-3) I=6 の場合:
E=9 となる。
百、千の位に注目すると、G×4+43=BB
これを満たす G は 3 であり、B=5 となる。
すなわち、46391×4=185564
| 4 | 8 | G | 7 | 1 | |
| x | 4 | ||||
| 4 | |||||
| 2 | 8 | ||||
| e | f | ||||
| 3 | 2 | ||||
| 1 | 6 | ||||
| 1 | 9 | B | B | 2 | 4 |
| 4 | 8 | G | 2 | 1 | |
| x | 4 | ||||
| 4 | |||||
| 8 | |||||
| e | f | ||||
| 3 | 2 | ||||
| 1 | 6 | ||||
| 1 | 9 | B | B | 8 | 4 |
7-4) I=8 の場合:
E=2 または 7 となる。
7-4-1) E=2 の場合:
百、千の位に注目すると、G×4+20=BB
これを満たす G は 6 であるが、B=T=4 となるので、E≠2
7-4-2) E=7 の場合:
百、千の位に注目すると、G×4+22=BB
これを満たす G は 0 であり、B=2 となる。
すなわち、48071×4=192284
以上により、7-3) と 7-4-2) の 2 つの場合が題意に適す。
答えは A,B,E,G,I,R,T の順に、8,5,9,3,6,1,4 または 9,2,7,0,8,1,4
27. ママはたいへんなのだ!(サラのママ さん)
世紀末を祝って 2000 人を招待したサラのママ。新年を迎えたらサラに 2001 人のお客さんを招待する事にしました。用意したケーキは均一な円の大きなチーズケーキ 2 つ。1 つのケーキは 2000 等分に切り分けて、世紀末から参加されたお客様用。もう 1 つのケーキは 2001 等分に切り分けて新年にお迎えしたお客様用。
ところが、いざ、皆さんで頂こうとするとお客様が、ケーキの大きさの違いに気が付いてご不満を……。仕方なくサラのママは、再度ケーキを切りなおすことに。
次のカッコに当てはまる数字を答えてください。
必殺サラのママ、ケーキ斬り:
- まず、世紀末ケーキ。2000 等分されたケーキをすべて ( ア ) 等分に切る。
- 1. で切り分けられたケーキを 2000 人のお客様が、新年にお迎えした 2001 人のお客様にそれぞれ 1 つずつお渡しする。
- 次に、新年向けケーキ。2001 等分されたケーキは、すべて ( イ ) 等分に切る。
- 3. で切り分けられた新年向けケーキを 2001 人のお客様が、世紀末から参加された 2000 人のお客様にそれぞれ 1 つずつお渡しする。
〔解答・解説〕お客さま一人ひとりが、自分のもっているケーキを全員の数で分割し、味の異なるケーキをもっているお客さまに差し出せばよい。
したがって、(ア)、(イ) ともに 2000+2001=4001
28. 世界一の人気者(田村 稔 さん)
世界にはディズニーのパークが 4 つあります。それぞれのパークには、ときどきミッキーマウスが出没し、みんなを楽しませてくれます。このことについて、昔から一つの噂があります。
「ミッキーマウスはこの世界に一人しかいないので、同時に二つ以上のパークには出現しないように管理されている」
そこで、この噂が本当だとして問題です。以下の条件のもとに、ミッキーマウスは最も長く存在できるパークに一日最大何分存在できるでしょうか?
- 4 つのパークとも 24 時間営業とする。
- あるパークに一回出現すると、そのパークに連続して 10 分以上 30 分以下の間、存在する。
- それぞれのパークを連続 1 時間を超えて留守にしない。
〔解答・解説〕ミッキーのいる時間が最大となるパークを A、その他を B、C、D とする。
また、各パークに時差があるかもしれないが、どのパークの出現時間もパーク A 時間で考えることにする。
まず、パーク B における出現時間が最小になるように考える。
1 時間を超えて留守にできず、最低 10 分間いなければならないので、最初の出現は 1:00 から 1:10、次は 2:10 から 2:20 というように、70 分ごとに 10 分間出現する。
24×60÷70=20 あまり 40 (分) より、全部で 20 回出現し、最後は 23:10 から 23:20。
次に、パーク C でも同様に、 70 分ごとに 10 分間出現すればよいのですが、パーク B と同時刻には出現できないので、10 分前にずらして、0:50 から 1:00、次は 2:00 から 2:10 というように、全部で 20 回出現し、最後は 23:00 から 23:10。
そして、パーク D でも同様に、パーク C の前に 10 分間出現しようとすると、残りのパーク A では 40 分連続になってしまうので、さらに 10 分前にずらして、0:30 から 0:40、次は 1:40 から 1:50 というように、全部で 21 回出現し、最後は 23:50 から 24:00。
パーク B、C、D での出現時間は (20+20+21)×10=610 (分) となり、これを 24 時間から引いて、24×60-610=830 (分)
29. 速さの問題(YokoyaMac さん)
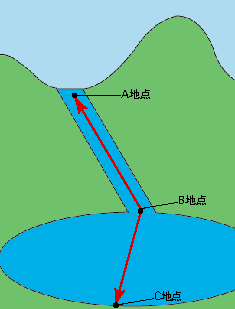
図のように川の上流に A 地点、下流に B 地点、湖の B 地点の対岸に C 地点があります(注 1)。A 地点から C 地点までの距離は 6000 m です(注 2)。
横山君は静水での速さが毎分 60 m のボートに乗って、AC 間を往復しました。すると、A 地点を出発してから B 地点を通って C 地点に到着するまで 90 分かかり、C 地点を出発してから B 地点を通って A 地点に到着するまで 120 分かかりました。
それでは、次の (1)、(2) の問いに答えてください。
(1) AB 間の川の流速は毎分何 m ですか。
(2) AB 間の距離は何 m ですか。
注 1:AB 間には一定の流速で水が流れていて、BC 間には水の流れはないということです。
注 2:A~B の最短距離と B~C の最短距離との合計が 6000 m ということです。
〔解答・解説〕縦軸に速さ、横軸に時間をとって図をかいてみる。
もし、毎分 60 m の速さで 6000 m 移動するとしたら、100 分かかるので、川の流れの速さを●で表すと、図 1 のような図がかける。ここで、黄色の部分、紫色の部分、水色の部分はすべて 600 m であることが分かる。
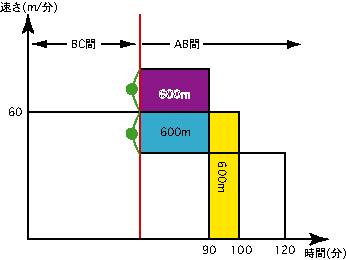
【 図 1 】
次に、100 分と 90 分の差 10 分と、120 分と 100 分の差 20 分の比は 1:2 であるから、図 2 において、オレンジ色の部分と青色の部分も 1:2 となる。また、青色の部分とピンク色の部分は等しい。
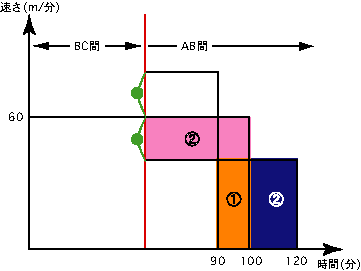
【 図 2 】
図 1 と図 2 を比べると、ピンク色の部分とオレンジ色の部分の合計は 1200 m であることが分かるので、図 3 のように、距離を書き込むことができる。
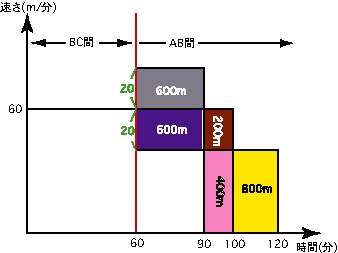
【 図 3 】
したがって、(1) 川の流れの速さは毎分 20 m、(2) AB 間の距離は 2400 m となる。
30. みんな大好き、立体の切断だよ !!(ありっち さん)
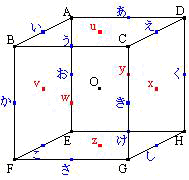
各辺の長さが 12 cm の立方体 ABCD-EFGH があります。点 あ~し はこの立方体の辺の中点、点 u~z は面の中心、点 O は立方体の中心です。
(1) 8 つの三角すい A-きさし、B-くけし、C-おこけ、D-かこさ、E-うえき、F-あえく、G-あいお、H-いうか の共通部分(重なる部分)の体積は何 cm³ ですか。
(2) 4 つの三角すい A-wxz、C-vyz、F-uxy、H-uvw の共通部分(重なる部分)の体積は何 cm³ ですか。
補足:それぞれ 8 つまたは 4 つの三角すい全てに共通する部分を考えてください。共通部分は立方体の中心 O を含みます。
よく似た問題(というか「元ネタ」)が、
にありますので、参考にして下さい。
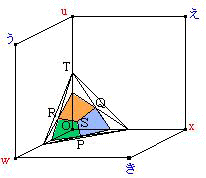
〔解答・解説〕
(1) 共通部分は合同な 24 個の面からなる立体となる。立方体を面に平行にたて横に切断し、小立方体 8 個に分けると考えやすい。右上手前の小立方体で考える(右図 1)。
- 小立方体 uうCえ-Owきx を、面 Gあい は Ou を O から 2 cm の点で、Ow を O から 3 cm の点で、Ox を O から 3 cm の点で切断する(赤色の面)。
- 面 Dかさ は Ou を O から 3 cm の点で、Ow を O から 2 cm の点で、Ox を O から 3 cm の点で切断する(緑色の面)。
- 面 Bくし は Ou を O から 3 cm の点で、Ow を O から 3 cm の点で、Ox を O から 2 cm の点で切断する(青色の面)。
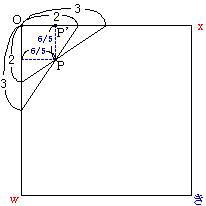
この他の面は中心 O から遠いので、以上の 3 面だけを考えればよい。
面 Dかさ と 面 Bくし と 水平面 Owx の交点 P から垂直面 Oux に下ろした垂線の足を P'、P から垂直面 Ouw に下ろした垂線の足を P'' とすると、比を考えて PP'=PP''=6/5 cm(右図 2)。
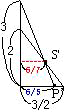
同様に、3 面の交点 S から垂直面 Oux に下ろした垂線の足を S'、S から垂直面 Ouw に下ろした垂線の足を S'' とすると、SS'=SS''=6/7 cm(右図 3)。
したがって、立体の 2 面(緑と青)と中心 O を通る水平面、垂直面がつくる四角すいの体積から、第 3 の面(赤)で切った外側の四角すい TRSQ の体積を引いて、12/5-12/35=72/35 (cm³)
これを 8 倍して 72/35×8=576/35 (cm³)
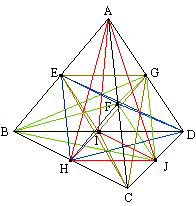
(2) 立体 ACFH は正四面体で、u~z は各辺の中点であるから、この問題は次のように言い換えることができる:
「右図 4 は体積 12×12×12×1/3=576 (cm³) の正四面体 ABCD で、E~J は各辺の中点です。4 つの三角すい A-HIJ、B-FGJ、C-EGI、D-EFH の共通部分(重なる部分)の体積は何 cm³ ですか。」
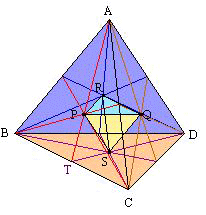
さて、しばし沈思黙考するか、正四面体を組み立ててみると(右図 5)、問題の立体は、各面の重心 P、Q、R、S を結んだ小さな正四面体 PQRS の各面の上に、背の低い三角すいを乗せた形と分かる。TP:PA=1:2 から、小さい正四面体 PQRS の高さはもとの正四面体の 1/3 である。
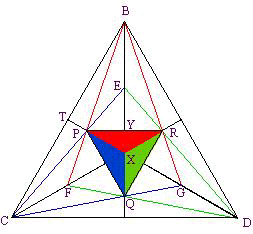
次に、背の低い三角すいの高さを求める。
もとの正四面体を面 PQR で切った面を真上から見ると右図 6 のようになる。
面 PQR の上に乗った背の低い三角すいの頂点を X、PR の中点を Y とすると、面 BFG が三角すいの面 PXR をつくる。
(言い換えると、B、P、R、X、Y、F、G は同じ平面上にある。)
Y から底面 BCD に下ろした垂線の足を Y'、X から面 PQR に下ろした垂線の足を X' とすると、X' は XS と面 PQR の交点。
BY':Y'S=5:1 より、YY':XX'=5:1
YY' は小さい正四面体 PQRS の高さと同じなので、背の低い三角すいの高さ XX' はもとの正四面体の高さの 1/3×1/5=1/15 (倍)
したがって、もとの正四面体の体積を 1 とすると、求める体積は小さい正四面体一つと背の低い三角すい 4 つであるから、1/3×1/3×1/3+1/3×1/3×1/15×4=1/15
もとの正四面体の体積は 12×12×12×1/3=576 (cm³) であるから、求める体積は 12×12×12×1/3×1/15=192/5 (cm³)
31. カードを配る問題(イデムリン さん)
1、2、3、4、5、6、… と 1 から順番に番号の書いてあるカードを、おそまつ、さくら、とどまつ、あやめ、からまつ、すみれ、じゅうしまつの 7 人に、おそまつ → さくら → とどまつ → あやめ → からまつ → すみれ → じゅうしまつ → すみれ → からまつ → あやめ → とどまつ → さくら → おそまつ → さくら → とどまつ → … の順に配ります。
ある番号のカードまで配ったとき、おそまつとからまつに配ったカードの枚数の差が 77 枚になりました。
このとき、とどまつの持っているカードの中で最も大きい番号は何番ですか?考えられるものを全て答えなさい。
〔解答・解説〕カードは下のように 12 枚一組で配られると考えられる。
| おそ | さく | とど | あや | から | すみ | じゅ | |
| 1 組目 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 12 | 11 | 10 | 9 | 8 | 7 | ||
| 2 組目 | 13 | 14 | 15 | 16 | 17 | 18 | |
| 24 | 23 | 22 | 21 | 20 | 19 |
一組配るごとに、おそまつとからまつの持っているカードの枚数の差は 1 枚ずつ増えていく。
よって、77 組目の 9 枚目まで配ったとき、おそまつとからまつの持っているカードの枚数の差ははじめて 77 枚になる。
そこで、77 組目以降を書き出して、くわしく調べてみることにする。
| おそ | さく | とど | あや | から | すみ | じゅ | |
| 77 組目 | 913 | 914 | 915 | 916 | 917 | 918 | |
| 924 | 923 | 922 | 921 | 920 | 919 | ||
| 78 組目 | 925 | 926 | 927 | 928 | 929 | 930 | |
| 936 | 935 | 934 | 933 | 932 | 931 | ||
| 79 組目 | 937 | 938 | 939 | 940 | 941 | 942 | |
| 948 | 947 | 946 | 945 | 944 | 943 |
からまつに 921 のカードが配られたとき、おそまつとからまつのもっているカードの枚数の差が 77 枚になり、とどまつのもっているカードの最大は 915 である。この状態は、おそまつに 925 のカードが配られるまで続くので、とどまつのもっているカードの最大が 923 のときもこの状態は続いている。
おそまつに 925 のカードが配られると、二人のカードの枚数の差はいったん 76 枚になるが、からまつに 929 のカードが配られると、差は再び 77 枚にもどる。このとき、とどまつのもっているカードの最大は 927 である。
からまつに 933 のカードが配られると、二人の差は 78 枚に増えるが、おそまつに 937 のカードが配られると、差はみたび 77 枚にもどる。このとき、とどまつのもっているカードの最大は 935 である。この状態は、からまつに 941 のカードが配られるまで続くので、とどまつのもっているカードの最大が 939 のときもこの状態は続いている。
からまつに 941 のカードが配られると、差は 78 枚にもどるが、その後、差が 77 枚になることはない。
したがって、答えは 915,923,927,935,939 である。
32. 題名は思いつかないなぁ(ちーくん さん)
10 をいくつかの自然数の和に分けます。(例えば 10=3+7、10=6+2+2)
そしてこの分けたものの積をとります。(上の例で言うと 3×7=21、6×2×2=24)
この積の中で最大値は何でしょう。
〔解答・解説〕1 は積を変えないので、1 をふくまない分け方を考える。
例えば、10=5+4+1 とすると、5×4×1=20 であるが、10=5+5 または 6+4 とした方が積は 20 より大きくなる。
1) 2 つに分ける場合:
- 2+8 → 2×8=16
- 3+7 → 3×7=21
- 4+6 → 4×6=24
- 5+5 → 5×5=25
2) 3 つに分ける場合:
- 2+2+6 → 2×2×6=24
- 2+3+5 → 2×3×5=30
- 2+4+4 → 2×4×4=32
- 3+3+4 → 3×3×4=36
3) 4 つに分ける場合:
- 2+2+2+4 → 2×2×2×4=32
- 2+2+3+3 → 2×2×3×3=36
4) 5 つに分ける場合:
- 2+2+2+2+2 → 2×2×2×2×2=32
以上により、積の最大値は 36 である。
33. 難問ぞろいの算トラ IV のオ・ア・シ・ス♪(KIN さん)
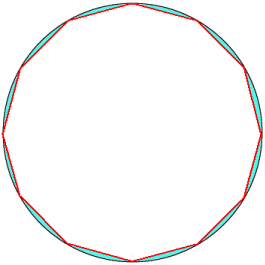

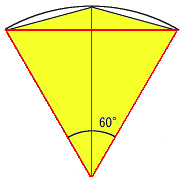
KIN君はマークを作ろうと下のような作業をしました。半径 10 cm の円周上に 12 個等間隔に点を打ちとなりどうしを結びました。(左上図)
そして、右上図の水色の部分を赤線を折り目として折りました。この時、2 枚重ねの部分と 1 枚のみの部分とが出来ますが、1 枚の部分だけを使うことにしました。これだけだと寂しいので、「KIN」という文字を入れることにしました。(右上図)
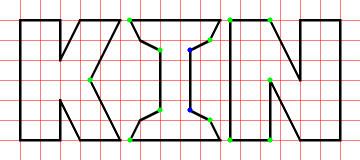 「KIN」という文字は 1 cm x 1 cm のマス目の方眼紙上に書くとこのようになります。(右図)
「KIN」という文字は 1 cm x 1 cm のマス目の方眼紙上に書くとこのようになります。(右図)
それでは、右上図の灰色の部分の面積は何 cm² ですか。
注:右図の青い点は 1 つのマスの中心、黄緑の点は一辺の中点です。
〔解答・解説〕求める面積は、(円の面積)-(水色の部分の面積)×2-("KIN" の面積) である。
 まず、水色の部分の面積を求める。
まず、水色の部分の面積を求める。
水色の部分の面積は、(円の面積)-(正十二角形の面積) であるから、正十二角形の面積を求める。
図のような正十二角形の一部分に注目する。これは正十二角形の 1/6 であり、中心角は 60° であるので、赤線の部分はすべて長さが等しい。
よって、黄色の部分の面積は 10×10÷2=50 (cm²) であり、正十二角形の面積は 50×6=300 (cm²)
また、円の面積は 10×10×3.14=314 (cm²)
したがって、水色の部分の面積は 314-300=14 (cm²)
また、"KIN" の面積は地道に数えて、67 cm² であることが分かる。
よって、求める面積は 314-14×2-67=219 (cm²)
34. 続・アルコール依存症(ぉ(Hamayan さん)
~私の千鳥足、そこにある電灯は一部始終を見ていたらしい。~
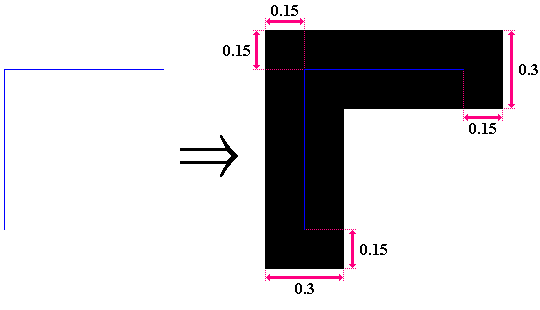
図 1 のように、長方形 PQRS の頂点 S の真上 9 m のところに点光源があります。図 2 のような光を通さない直方体があり、KL と PQ が常に平行になるようにして、底面の正方形 KLMN の対角線の交点 O が長方形 PQRS 上の青線(図 3)上を、A 点から B 点まで滑って移動したとき、長方形イロハニ上で常に光が当たっていた部分の面積は ( ? )/64 m² となります。
( ? ) に当てはまる数値を求めなさい。図中の数値の単位はすべてメートルです。滑って移動する様子が分かりづらいかもしれませんが、たとえば、青線が図 4 左のようにあるとすれば(青線は PQ または PS に平行)、図 4 右の黒く塗りつぶしたところが正方形 KLMN の通った部分になります。
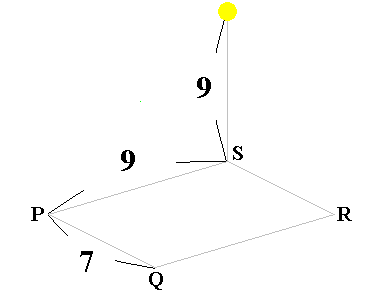
【 図 1 】
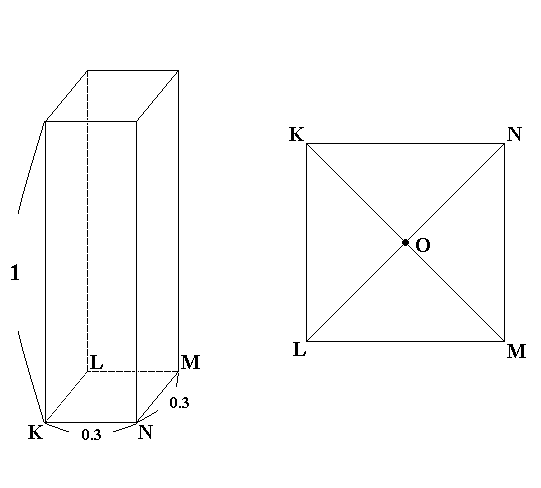
【 図 2 】
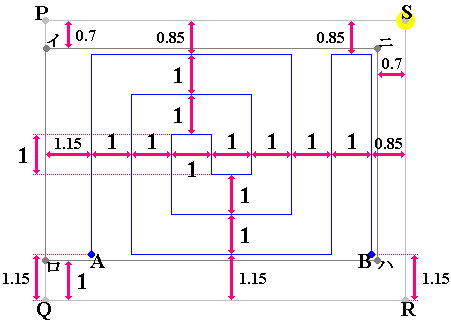
【 図 3 】
【 図 4 】
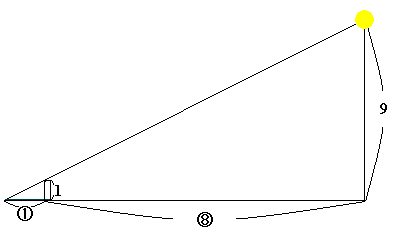
〔解答・解説〕横から見ると、影になるのは右図の①の部分および直方体の底面。
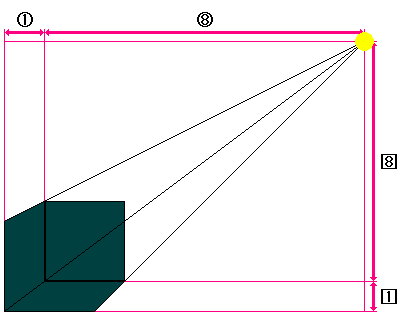
真上から見ると、影になるのは右図の黒色部分。

直方体が青線の上を通ったとき、影になるのは右図の黒色部分。
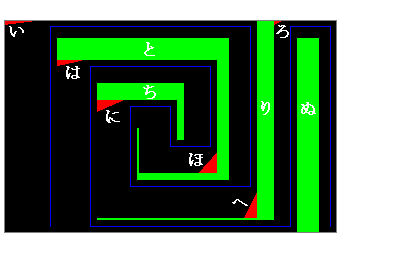
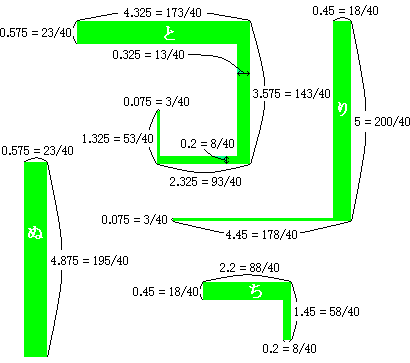
長方形イロハニ内でいつも光が当たるのは、右図の赤色と緑色の部分。
赤色の直角三角形について、PS に平行な辺を底辺とみて(単位は m)
| 底辺 | 高さ | |
| い | 8×1/8 | 0.7×1/8 |
| ろ | 2×1/8 | 0.7×1/8 |
| は | 0.7 | 0.7×1.7/7 |
| に | 0.7 | 0.7×2.7/6 |
| ほ | 3.7×1/8 | 4×1/8 |
| へ | 2.7×1/8 | 5×1/8 |
また、緑色の部分については右図の通り。
したがって、求める面積は い+ろ+は+に+ほ+へ+と+ち+り+ぬ=699.834/64 (m²)
